Solar System Model View

Kepler's Laws

Early in the 17th century, Johannes Kepler discovered three laws which described the motion of the planets. These laws were unexplained at the time, but were of such importance that they still bear his name. He derived these laws by analyzing the extensive observations of the planets made by Tycho Brahe in the years preceding. These laws are:
  1. The orbit of each planet is an ellipse with the sun at one of its foci.
    A circle is a special case of an ellipse with both foci at the center.
  2. The radius vector of each planet describes equal areas in equal time.
    For an ellipse the radius vector would be the line from the Sun (at one focus) to the planet.
  3. The squares of the periods of the planets are proportional to the cubes of their mean distances from the Sun.
    This is sometimes called the harmonic law.
The implication of the second law is that the force which controls the orbit of a planet is directed along the line between the planet and the sun. Newton then was able to show, from the fact that the orbit is an ellipse, that the force acting on each planet at different points in its orbit varies inversely as the square of the radius vector between the planet and the Sun.

Then, from the third law, Newton was able to prove that the forces acting on the planets are inversely proportional to the squares of their distances and directly proportional to their masses. This fact is easy to demonstrate for circular orbits. We begin with the equation for the force on a body in circular motion:

f = mV2 / r

and substituting V = 2pi r / t      (circumference /time)

f = 4 pi2 m r / t2

Then, using the subscripts 1 and 2 for planets 1 and 2,

f1 / f2 = m1 r1 t22 / m2 r2 t12

But from Kepler's third law,

t22 / t12 = r23 / r13

Substituting this relationship into the previous expression:

f1 / f2 = m1 r22 / m2 r12

describing the propertirs of the gravitational force.

For the case of elliptical orbits, a, the semi-major axis of the orbit, is substituted for r, but the derivation of this relationship is much less simple.

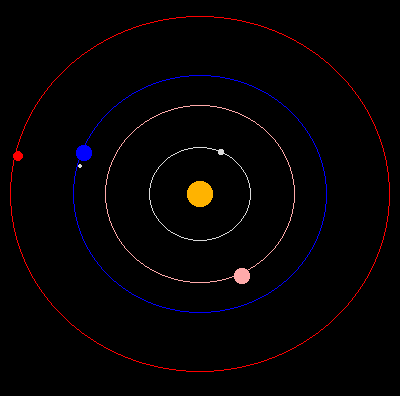
In the figure above we see the inner 4 planets in our solar system and our moon. The physical parameters of these planets are given in the table below.

Planet Mass Orbit Radius Period Eccentricity
(kg) (km) (days)
Mercury 3.31 × 1023 5.79 × 107 87.97 0.206
Venus 4.87 × 1024 1.08 × 108 224.70 0.007
Earth 5.98 × 1024 1.50 × 108 365.26 0.017
Mars 6.43 × 1023 2.28 × 108 686.98 0.093
[email protected]